Anyone for Tennis... and Game Theory?
A great illustration that game theory's predictions help make sense of behaviour in the real world
As I pointed out in one of the initial posts of this Substack, behavioural scientists have, in recent years, often proposed to explain the quirks of human behaviour with the existence of cognitive biases leading people towards predictable mistakes and inefficient decisions. In contrast to this perspective, studies that examine human behaviour in real-world contexts often find that people can be surprisingly adept at solving complex problems. In this post, I’ll illustrate this with a setting familiar to most readers: tennis.
Tennis ranks among the most popular sports worldwide. Its major tournaments attract significant attention, and players such as Federer, Nadal, and Djokovic have become household names. Furthermore, tennis offers a wealth of observed data, with players interacting in well-defined, strategic situations. This makes it a fertile ground for investigating the ability of game theory—the study of strategic behaviour in social interactions—to predict actual behaviour in the real world.
The rules of tennis may seem simple to grasp, and, as spectators, we often feel we understand what's happening in the games we watch. We might even catch ourselves thinking, “you should have hit here” or “why did you try that shot?” as though we were armchair coaches with insights the player missed.
In reality, however, watching professional athletes can create the illusion that what they do is much simpler than it truly is. Tennis is a case in point. The athletes' physical prowess, easily underappreciated on TV, is matched by decision-making skills that are often more sophisticated than commonly realised. In this post, I’ll show how research has found that professional tennis players are master strategists, to a point that is likely to surprise you.
Players mix their serves to be unpredictable… in the way predicted by game theory
If you have played tennis, you understand the importance of keeping your opponent guessing about where you'll place the ball next. But achieving unpredictability can be a complex task. If you adopt a particular strategy, your opponent may quickly adapt and begin to anticipate your next moves. Game theory pioneers von Neumann and Nash devised a solution, showing that it's possible to remain unpredictable without giving your opponent an incentive to change strategy, nor a need for you to alter yours. As I explained in my post introducing game theory, the key is to introduce randomness into your play.
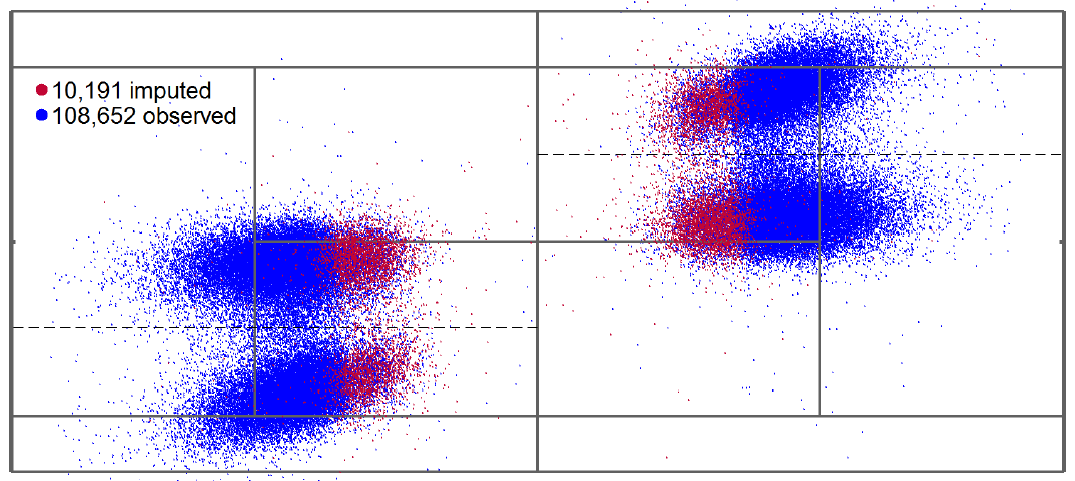
Let’s consider the case of choosing how to serve. The serve is among the most potent shots in tennis, with male players having about a 2/3 chance of winning a point when they serve. The rapid speed of the serve necessitates quick reactions from the receiver, who must respond to the ball's initial trajectory as swiftly as possible.1 A key decision for serves is their locations. The figure below shows the directions of first serves for male professional players. The blue dots are observed and the red dots are the intended directions of serves that ended up in the net. These serves cluster into two main areas, either in the middle of the court (“down the T”), or towards the side (“wide”).
Are players unpredictable when serving, in the way predicted by game theory? For this to be the case, they need to randomise and serve with some probability in the middle or wide. In the data displayed in the figure above, male players served around 55% of the time in the middle and 45% of the time wide. So, are the players randomising according to the prediction of game theory? How could we know if this is the case?
Game theory suggests that good strategic players would end up playing an equilibrium of the game, referred to as Nash equilibrium. It is a stable situation where players lack the incentive to alter their strategy and expectations. When considering the choice of a serving direction as a strategic game, an equilibrium can only be achieved if the server selects very specific probabilities for serving in each direction, effectively making the opponent indifferent between the two directions.2 A simple test can ascertain whether servers are adhering to a Nash equilibrium: if they are, their winning percentage should be identical in both directions. Intuitively, if the winning percentage was higher in one direction, the server would have an interest to serve more in that direction. Consequently, the receiver would anticipate this and adjust accordingly. The only scenario in which neither player has an interest in altering their strategy is when the winning percentage is equally balanced in both directions.
In a seminal paper that examined over 3,000 serves from 10 high-profile matches, including mostly grand slam finals, Mark Walker and John Wooders (2001) discovered evidence indicating that players seem indeed to be adhering to equilibrium play.3 Two decades later, Romain Gauriot, John Wooders, and I reexamined this classical finding. Utilising modern ball-tracking technology, we compiled a larger dataset, encompassing nearly 500,000 serves over more than 3,100 matches. Despite this expansive dataset enabling us to identify even small deviations from equilibrium play, we detected… none! Instead, our findings revealed that the directions in which players served were remarkably consistent with Nash equilibrium predictions. Players seem to closely equalise the winning probability in each serve direction, in each match they play.4
Interestingly, upon examining different categories of players, we observed that junior players deviate significantly from equilibrium play: they fail to perfectly approximate the winning probabilities for each serve direction. This finding is important. It implies that professional players have either learned to adhere to equilibrium play or have been selected for their ability to do so. In the latter case, perhaps only the most strategically astute junior players—able to follow equilibrium play—were able to reach the professional level.

Another noteworthy finding is that professional female players deviate slightly from equilibrium play. This deviation could potentially be due to gender differences in strategic behaviour. However, a simpler explanation might be that, owing to the slower serve speeds in women's matches,5 players possessing exceptional skills in other areas can compensate for minor deviations from equilibrium play on serves.
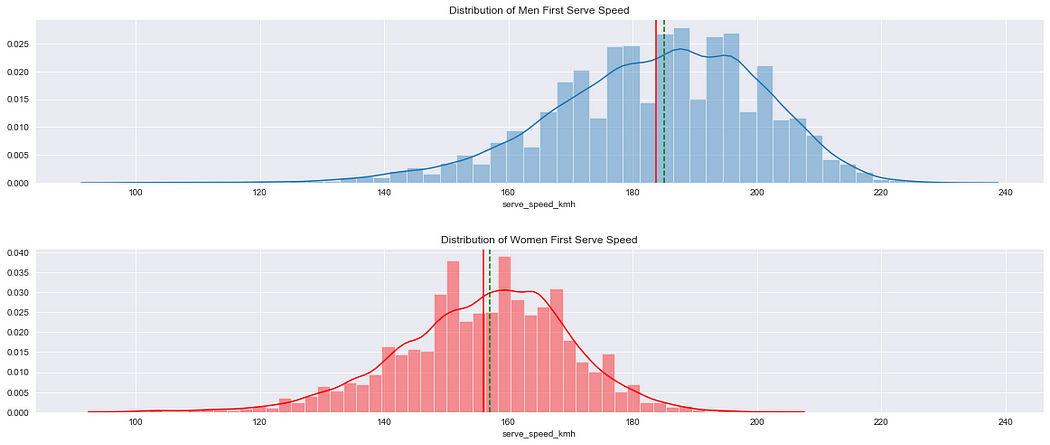
Most interestingly, we discovered that when the female receiver is a top-ranked player, the winning probabilities are equalised. This suggests that these elite players act to balance the servers' winning probabilities, in alignment with equilibrium predictions. Noticeably, this finding indicates that the behaviour of better players conforms more closely to theoretical expectations.
Players allocate effort strategically across points…
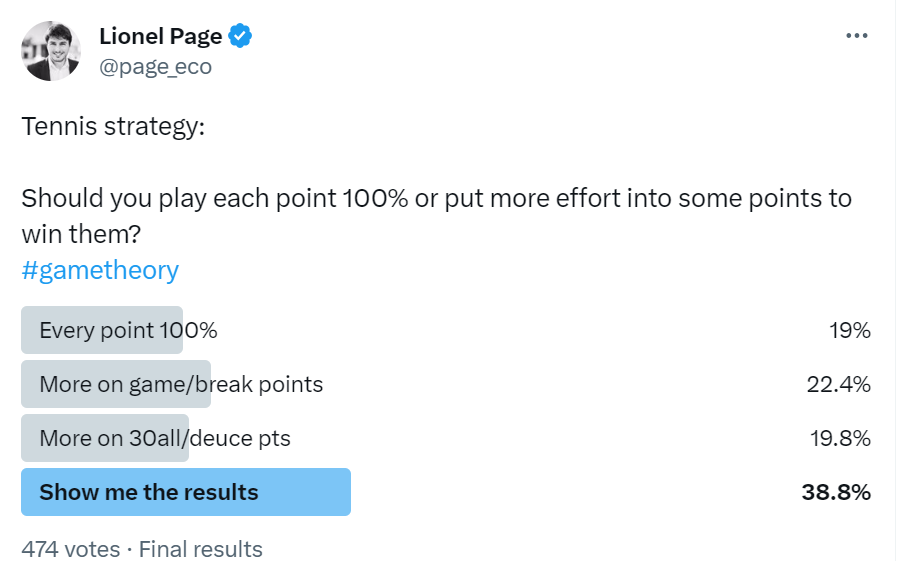
Sporting contests are typically effortful and thus provide an opportunity to study how players distribute their effort during the game. In tennis, for example, should a player expend 100% effort on every single point, or should they strategically allocate more effort to certain points? I posed this question in a poll on Twitter.
Most people thought that players should put more effort on game points and break points. Interestingly, professional players often publicly claim they strive to put 100% effort into every point. Djokovic, for example, expressed this idea in 2013 after winning a match at the US Open.
Such statements contrast with the predictions of game theory, which suggest that players should strategically vary their effort as a function of the importance of the points. This statement might be perplexing to some readers and thus warrants further explanation. One might question whether effort is indeed costly in a tennis match. Several factors contribute to this cost. Firstly, maximal effort can be inherently unpleasant as top performance is often strenuous and requires an individual to push beyond their comfort zone. This immediate discomfort is perhaps the first cost that comes to mind, and it may be commonly overlooked based on the assumption that professional players can ignore this cost, especially when the stakes are high.
There are other considerations though that contribute to the cost of effort within a match. Exerting more effort on certain points may lead to fatigue, which can adversely affect performance later on. This subsequent decline in performance represents an implicit cost of exerting effort on a given point. Players may therefore strategically conserve energy on less vital points to enhance their performance on crucial ones.
Extreme exertion may also carry consequences that extend beyond individual matches, such as an increased risk of injuries throughout the season. This can lead to fewer matches played in the future and represents another implicit cost of effort. The risks associated with such decisions are far from trivial, with one study identifying a 2% chance of injury per set.6

Let’s assume that the arguments above have convinced you that effort can be costly. The second reason why players strategically allocate their effort is that not all points have the same significance for the overall probability of winning the match. Imagine you are serving with a score of 40-0. Whether you win or lose that point you’ll still most likely win that game. Therefore, losing a point at 40-0 doesn't substantially alter your chances of victory. Contrast this with a situation where you are serving at 30-30. In this case, the winner of the point will be on the brink of winning the game, so the outcome of a point played at 30-30 becomes far more consequential for the final result of the game.
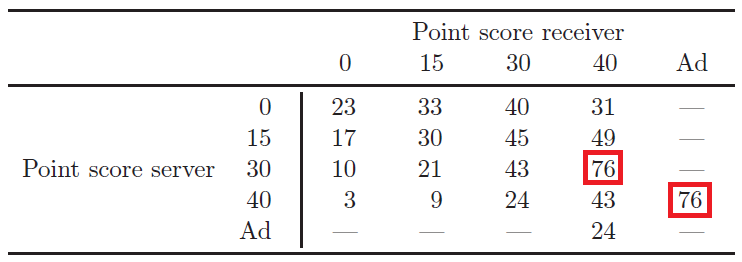
Carl Morris (1977) suggested following this line of thought and measuring the importance of a point in tennis by the effect of winning this point on the player’s probability of winning either the game, the set, or the match.7 Using this approach in a game, the most important points are breakpoints. For instance, the table below illustrates a situation where the server has a 64% chance of winning each point. Under these conditions, the server's probability of winning the game when the score is at deuce is 76%. Consequently, saving a breakpoint would give the server a 76% chance of winning the game, as opposed to 0% when losing that point.
Game theory goes one step further: If the stakes vary across points, then players should vary their effort across points. This implies that the probability of winning a point on serve should not be the same for all points. By extending contest models to tennis games, my colleague Romain Gauriot and I demonstrated that an equilibrium exists in this context, defining the level of effort players would exert on each point. From this analysis, we derive two predictions:
Momentum: The probability of winning the next point should increase after winning the current point.
Important points: The most important points tend to be 30-30 and deuce.8
The momentum effect is similar to the hot hand phenomenon in basketball. It arises here from the fact that, for a given point, the stakes for the trailing player are smaller (as they play to catch up) compared to the stakes for the leading player (who plays to win). The existence of momentum means that the player leading has a relatively higher winning probability than before. This fact influences the determination of the most important point in a game. After 30-30, the server’s winning probability diverges: It increases after a win and it decreases after a loss. This divergence in winning probabilities after 30-30 tends to make these points the most important of the game, instead of the breakpoints.
Using ball-tracking data on 3,100 matches, we examined situations where a point was either “just won” or “just lost”," and where the result might be attributed to chance. Specifically, we analysed points landing very close to the court's boundary line, either just in or just out.

Putting the ball just in, instead of just out, increases the player’s probability of winning the current point by 60%. In addition, we find that it also increases the probability of winning the next point by 4 percentage points! We can infer from this result that winning a point likely increases the probability of winning the next one by 7 percentage points.9 There is therefore evidence of momentum!
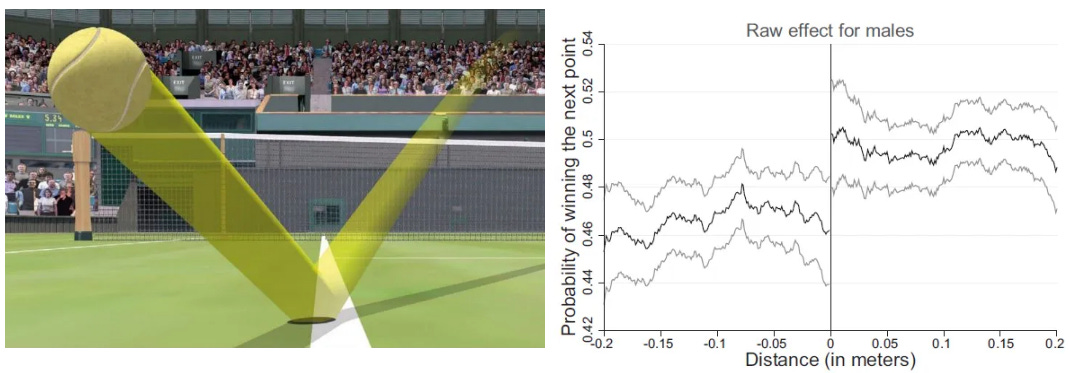
The observed momentum aligns with the variations in efforts that players are predicted to exert when playing according to equilibrium principles. We can further scrutinise the equilibrium predictions by examining whether players indeed exert more effort on the most crucial points. This is precisely what we discovered: players appear to exert more effort during the critical 30-30 and deuce points!
Additional support for our model's predictions can be found in insights provided by the highly successful player and later coach Brad Gilbert. In his book Winning Ugly, which delves into the psychology and strategies of tennis, he specifically identifies the 30-30 and deuce points as the most critical ones in a game.
…across sets…
The prediction of momentum applies not only to points but also to entire games and sets. For example, if you find yourself down 5-0 in a set, you may be better off saving your effort for the next set. Similarly, if you are trailing by one set, pushing yourself to the limit in the following set might not be the best strategy over the season, particularly if you're still likely to lose that set. We should therefore expect that players winning the first set become more likely to win the next set.
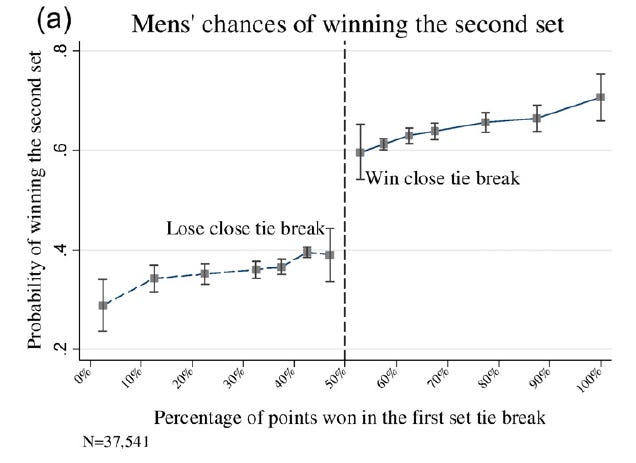
Malueg and Yates (2010) found results compatible with this prediction by looking at 100 matches where players were of similar strength and where the first set was close, going beyond the score of 5 games all. John Coates and I (2017) found further support for this prediction by looking at 617 matches in which the first set ended in an extremely close tie-break, with scores of 11-9 or higher. Even though the winners and losers of such close tie-breaks tend to be very close in strength, we found that a male player who wins the first set has a 60% chance of winning the second set.10
… and across matches
Finally, players should be mindful of expending their effort strategically across matches in a tournament. Have you ever pondered why favourites seem to uncharacteristically grapple against weaker opponents in the first week of Grand Slam tournaments? The explanation is that it is optimal for them to conserve energy for later rounds. This approach carries with it a higher risk of unexpected defeats in the initial rounds, where lesser-known players may be exerting their utmost effort, as they don't anticipate needing to conserve energy for many subsequent matches (Harbaugh and Klumpp, 2005).
In conclusion, from mixing tennis serves to allocating effort across points, sets and matches, professional players have been found to be surprisingly good at approximating the predictions from game theoretic models of strategic behaviour. When watching tennis matches, many of us have ventured into some armchair coaching, thinking that we could tell the player what he/she should do. The reality is that players are experts at playing strategies which we typically have little insights about. In that regard, tennis is a great example of how game theory can help make sense of behaviour in real-world strategic interactions.
This is the first post of a series showing how game theory often helps us make sense of the behaviour we observe in a wide range of social situations.
References
Aviles, C., Navia, J.A., Ruiz, L.M. and de Quel, Ó.M., 2019. Do expert tennis players actually demonstrate anticipatory behavior when returning a first serve under representative conditions? A systematic review including quality assessment and methodological recommendations. Psychology of Sport and Exercise, 43, pp.16-26.
Gauriot, R. and Page, L., 2019. Does success breed success? A quasi-experiment on strategic momentum in dynamic contests. The Economic Journal, 129(624), pp.3107-3136.
Gauriot, R., Page, L. and Wooders, J., 2023. Expertise, gender, and equilibrium play. Quantitative Economics, 14(3), pp.981-1020.
Gilbert, B. and Jamison, S., 2013. Winning Ugly: Mental Warfare in Tennis--Lessons from a Master. Simon and Schuster.
Harbaugh, R. and Klumpp, T., 2005. Early round upsets and championship blowouts. Economic Inquiry, 43(2), pp.316-329.
Klaassen, F. and Magnus, J.R., 2014. Analyzing Wimbledon: The power of statistics. Oxford University Press.
Konrad, K.A., 2009. Strategy and dynamics in contests. OUP Catalogue.
Kvålseth, T.O., 1987, September. Stimulus probability, surprise, and reaction time. In Proceedings of the Human Factors Society Annual Meeting (Vol. 31, No. 2, pp. 147-150). Sage CA: Los Angeles, CA: SAGE Publications.
Malueg, D.A. and Yates, A.J., 2010. Testing contest theory: evidence from best-of-three tennis matches. The Review of Economics and Statistics, 92(3), pp.689-692.
Morris, C., 1977. The most important points in tennis. Optimal strategies in sport, pp.131-140.
Page, L. and Coates, J., 2017. Winner and loser effects in human competitions. Evidence from equally matched tennis players. Evolution and Human Behavior, 38(4), pp.530-535.
Triolet, C., Benguigui, N., Le Runigo, C. and Williams, A.M., 2013. Quantifying the nature of anticipation in professional tennis. Journal of Sports Sciences, 31(8), pp.820-830.
Walker, M. and Wooders, J., 2001. Minimax play at Wimbledon. American Economic Review, 91(5), pp.1521-1538.
Woodford, M., 2012. Inattentive valuation and reference-dependent choice.
The evidence does not suggest that tennis players anticipate the service directions with pre-emptive movements (Triolet et al. 2013, Aviles et al. 2019) but reaction times are a function of expectations and a player’s reaction time in one direction would credibly be slower in a direction it expects to occur less frequently (Kvålseth 1987, Woodford 2012). A receiver’s expectations can therefore be considered as the receiver’s move in the game of returning serve.
Or more precisely between anticipating one or the other direction.
The tests are not only for each player in each match but also for each serve box (deuce and ad courts) for which players may have different payoffs over the two directions given that the angles are different for the server, and that a wide vs T directions will likely lead to a different stroke by the receiver (forehand vs backhand).
We nonetheless observed some deviations in the fact that players tended to alternate directions in a slightly too predictable way: the probability of serving in one direction decreased after having served in that direction on the previous serve.
In our dataset, the average speed of the first serve is 160 kph for men and 135 kph for women. Only 0.45 seconds elapse between the serve and the first bounce in men’s tennis!
This number may seem small, but it means 30% to 40 % of injuries per match! Many injuries do not prevent playing, but they hinder performance. This high risk of injury may be heightened by the fact that the observations were made in a Grand Slam where players may be more willing to push themselves to their limit due to the high stakes.
To do these calculations, this approach assumes for simplicity that the probability of a player winning his/her serve is constant across points.
Note that these points are strategically equivalent: they both require a player to win two points in a row to win the game.
In practice, a player does not always lose when the ball is just out as line umpires sometimes fail to call the ball out. Similarly, a player does not always win when the ball is just in as the other player may return the ball. Putting the ball just in vs. just out increases the player’s chance to win the current point by around 60 percentage points. It is this increase that is associated with the 4 percentage points increase in the probability of winning the next point. Using the Wald estimator in a fuzzy regression discontinuity design (that corresponds intuitively to a proportional rule) we can estimate the full effect of winning the current point (i.e. if your probability of winning the current point goes from 0 to 100): 0.04/0.6=0.07.
Noticeably we do not find a significant effect for female players.





Thanks for this super insightful post Lionel! Just one question: how is players' effort measured in the studies mentioned in that second part of the post? I imagine it can take many forms (e.g., riskier serves, holding longer in a rally, faster shots, etc.)