The game theoretical foundations of morality
The good reasons why we care about reciprocity
One of the primary notions associated with economics is that it relies on the assumption that people are selfish and care only about their material self-interest. This view is often held by critics of economics, but also by many economists themselves. When discussing whether people adhere to ethical values, Nobel Prize winner George Stigler stated, "Much of the time, most of the time in fact, the self-interest theory… will win." (1981).
Much of the time, most of the time in fact, the self-interest theory… will win. - George Stigler (1981)
However, the belief that economics relies on, or must rely on, the assumption that people are selfish is strange. Indeed, one of the fundamental explanations of why we care about moral principles has been offered by a central approach in economics: Game theory. As behavioural economics – the integration of psychological insights into economics – has shown, people do care about others and do not behave as asocial egotists. Today, we'll dive into the game theoretical roots of morality and see how our moral intuitions are not “irrational”. Instead, our moral intuitions most likely evolved to successfully navigate the challenges of social interactions.
Game theory is the study of rational behaviour in strategic interactions, where people aim to make the best decisions given what others are doing (themselves trying to make the best decisions given what others are doing). In my first Substack post, I discussed the history of one of the most iconic games studied in game theory: the Prisoner's Dilemma. This classic game theory conundrum is often used to highlight the difficulty of cooperation. Let's revisit this game. It presents a hypothetical scenario where two individuals are arrested for a crime and held in separate cells. They cannot communicate with each other and must make a decision independently - to confess or stay silent. If both stay silent, they serve a short sentence (for example, one year) due to lack of evidence. If both confess, they serve a longer sentence (for example, five years), but less than they would if one confesses and the other doesn't. If one confesses and the other stays silent, the one who confesses goes free, while the other receives the longest sentence (for example, twenty years).
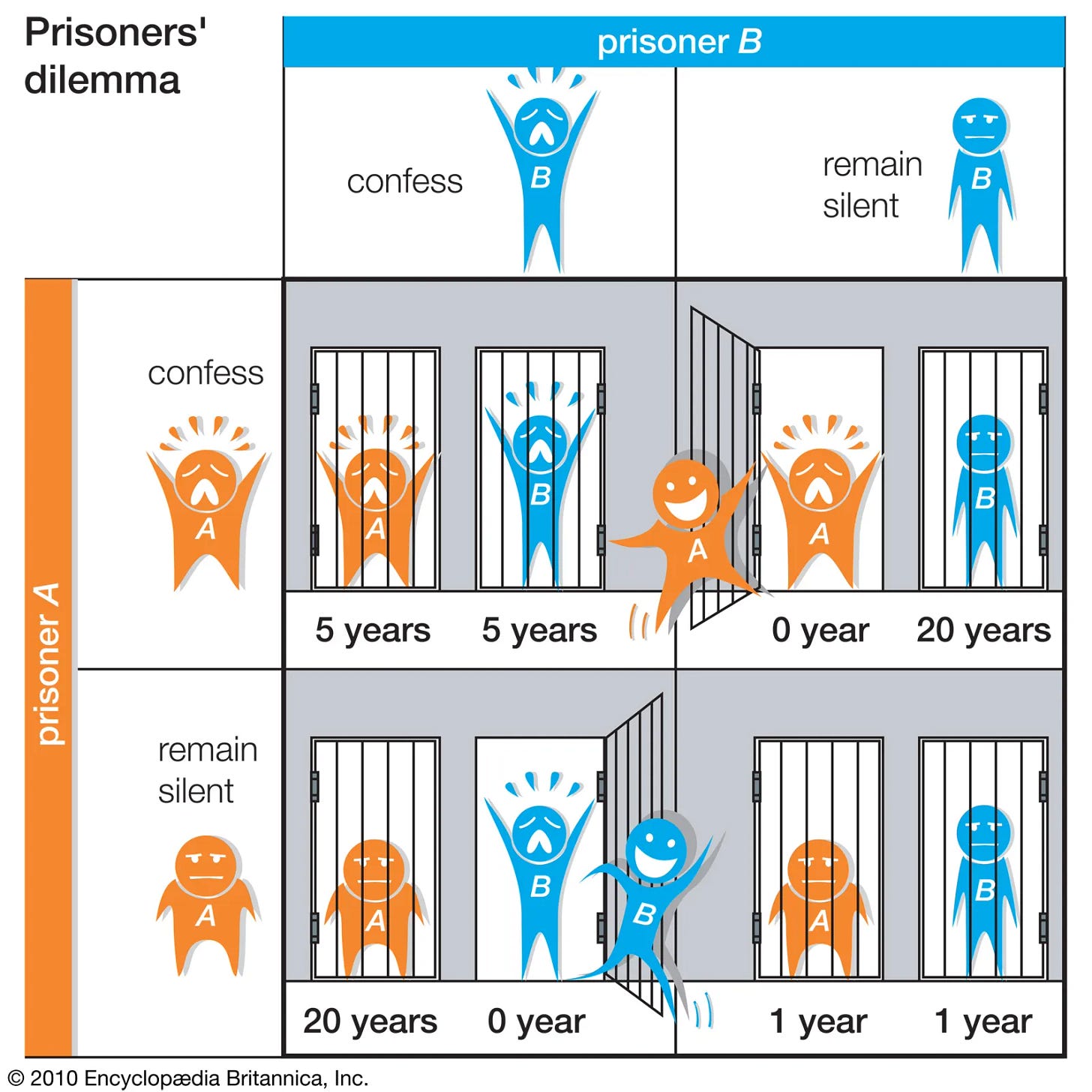
Even though both would be better off if they both remained silent, individual logic dictates that they confess. It is because, whatever the other does, each prisoner gets a lighter sentence when confessing. As such, the (self-centred) rational decision is to confess. This leads to a collectively undesirable outcome, where both confess and receive a harsher punishment than if they had cooperated and stayed silent. The essence of the dilemma lies in the fact that both prisoners would ideally prefer mutual cooperation and silence; however, their individual rationality inevitably may drive them to defect and confess.
However, as I previously pointed out, when the Prisoner's Dilemma is repeated, cooperation naturally arises. This fact paves the way for a fascinating exploration of the connection between game theory and morality. The emergence of cooperation in the Prisoner’s Dilemma is not a fluke, it is backed by a widely known result, the Folk Theorem, a cornerstone of game theory that shows how cooperation can be rationally sustained in repeated interactions. The key idea from the Folk Theorem is simple: if individuals value the potential future benefits of sustained cooperation, it can be rational for them to resist the temptation to defect in the present. Trying to take advantage of others now can bring benefits in the short term, but it may also mean losing their trust, their willingness to cooperate in the future, and therefore the stream of future rewards from cooperation. The risk of losing future opportunities to cooperate can therefore act as a deterrent, enforcing cooperative behaviour in the present.
To illustrate this, consider one possible way to play in the repeated Prisoner’s Dilemma game, which game theorists call the "grim strategy." It is characterised by zero forgiveness for defection. When players follow this strategy, they start by cooperating and continue to do so as long as their counterpart does the same. However, if the other player defects, the grim strategy player will cease to cooperate in all future interactions. While this strategy is quite harsh, an interesting consequence is that when both players follow this strategy, neither of them has the incentive to defect, and therefore they engage in stable cooperation over time.

The Folk Theorem’s name comes from the fact that, in the 1950s, game theorists became aware of the idea of the theorem without knowing exactly who precisely had come up with the idea in the first place. Earlier statements of the possibility of rationally cooperating in repeated interactions were made by Luce and Raiffa (1957), Shubik (1959), and Aumann (1960), with the latter considered to have offered the theorem's first formal articulation. During their seminal exploration of this topic, Luce and Raiffa (1957) contested the notion of joint defection as the "solution" to the repeated prisoner's dilemma. Instead, the choice to cooperate appeared to them to be a solution, even though it “is extremely unstable; any loss of ‘faith’ in one’s opponent sets up a chain which leads to loss for both players”.

Aware of these discussions in economics (and of Luce and Raiffa’s reflections, in particular) the biologist Robert Trivers published in 1971 one of the most influential articles in the history of biology, “The Evolution of Reciprocal Altruism.” In it, Trivers builds on the insight that cooperation can emerge when interactions are repeated to propose an explanation of altruism between strangers. Trivers’ article presents a rich set of ideas about how individuals would regulate cooperation through the reward of cooperative behaviour and the detection and punishment of uncooperative behaviour.
Under certain conditions natural selection favors these altruistic behaviors be- cause in the long run they benefit the organism performing them. - Robert Trivers 1971
The implications of the Folk Theorem are profound. This result suggests that even purely self-interested players can rationally engage in sustained cooperation over time if the probability of future interactions is high enough. It challenges the traditional view of the economic approach, which posits that human interactions should be dominated by uncooperative behaviour due to players' selfishness.
The predictions of the Folk Theorem were later complemented by a famous study by the political scientist Robert Axelrod, who organised competitions between strategies playing the repeated prisoner's dilemma. These tournaments aimed to determine the best strategy able to maximise rewards over time. Each strategy played against every other strategy once, over 200 moves. Economists, sociologists, psychologists, mathematicians and political scientists were invited to submit strategies to the tournament. Some strategies were quite complex, attempting to model the strategy of the other player from past actions to infer the best action to play. The result of this study was unexpected and astonishing. The most successful strategy ended up being one that even a three-year-old toddler can understand: tit-for-tat. It starts by playing cooperating in the first period. After that, it follows a simple rule: it cooperates with players who have cooperated in the previous period and it defects with players who have defected in the previous period.
This result is fascinating for two reasons. First, it is a surprisingly simple strategy among all the possible strategies one could think of. Second, it is surprisingly intuitive. Tit-for-tat is a simple rule of reciprocity that can be described by a few human-like traits. It is nice: it starts by cooperating and continues to cooperate with cooperators. It is not a pushover: it retaliates against defectors. It is forgiving: it retaliates only once after a defection then cooperates again.
What accounts for tit-for-tat's robust success is its combination of being nice, retaliatory, forgiving, and clear. - Axelrod (1984)
Throughout history, we find expressions reflecting a tit-for-tat logic in social interactions. The Law of Talion, one of the oldest recorded laws dating back to Babylonian times, states that retaliation should be in proportion to the offence: "an eye for an eye." The reciprocity of the Law of Talion can be found in the oldest known code of law, the Code of Hammurabi from 1750 BCE.


In subsequent studies, Axelrod and others found strategies that perform better than tit-for-tat. An interesting feature of these winning strategies is that they are also intuitive. The gradual strategy by Beaufils et al. (1997) seems to be the most successful so far. It behaves like tit-for-tat, but it has a perfect memory of the other player’s past defections. It punishes any new defection by defecting a number of times equal to the number of past defections from the other player. This strategy can be seen as ramping up punishment towards players who do not change their behaviour after being sanctioned for their uncooperative behaviour.
The fact that these automatic rules can be easily understood using moral concepts such as reciprocity and forgiveness raises the prospect of a fascinating change of perspective. If we have the moral intuitions we do, it may be because they are solutions to the problem of cooperation in repeated interactions. It would then make sense that we find the strategies successful at this game “intuitive”; these rules may actually form the foundations of our moral intuitions. Armed with such intuitions, we may be able to successfully cooperate with others in games with repeated interactions.
In retrospect, the assumption of selfishness seems naive. Social interactions require collaboration and cooperation with others. Selfishness and egotism are not traits associated with the ability to interact fruitfully with other people. Cooperating and caring about others is not, in that sense, “irrational”. Our moral intuitions and our attachment to reciprocity may make us better at navigating successfully our way through social interactions.
I provide further insights on the game theoretical roots of morality in my recently published book, "Optimally Irrational," which delves into the good reasons behind the rich and subtle complexity of human behaviour.


